Given a 2D board and a list of words from the dictionary, find all words in the board.

Each word must be constructed from letters of sequentially adjacent cell, where “adjacent” cells are those horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

Example:
1
2
3
4
5
6
7
8
9
10
Input: 
board = [
  ['o','a','a','n'],
  ['e','t','a','e'],
  ['i','h','k','r'],
  ['i','f','l','v']
]
words = ["oath","pea","eat","rain"]

Output: ["eat","oath"]

解题思路：

DFS ：纯DFS就和后面word search I 是一样的，只不过这里给出了一个list的单词，我们需要针对这个list里面所有的单词来找。这个方法刚才在python里面尝试是超过时间限制的。那么看一下第二种

DFS+Trie：字典树的好处在于，如果我们有很多单词的前缀都一样而且特别长，字典树可以帮我们在board里面只寻找一次。

首先要知道如何构建字典树。

字典树首先是一个有很多level的树，且每个level的branch的数量都是26（对于单词来说）。
字典树需要具备的方法是插入单词和查找单词。
字典树中每一个节点需要是一个dict 且需要具备的性质是知道自己是否为一个单词。

# Build Trie
class TrieNode():
    def __init__(self):
        self.children = collections.defaultdict(TrieNode)
        self.isword = False
class Trie():
    
    def __init__(self):
        self.root = TrieNode()
        
    def insert(self, word):
        
        start = self.root
        for w in word:
            start = start.children[w]
        
        start.isword = True
        
    def search(self, word):
        start = self.root
        for w in word:
            start = start.children.get(w)
            if not start:
                return False
        
        return start.isword
            

class Solution(object):
    def findWords(self, board, words):
        """
        :type board: List[List[str]]
        :type words: List[str]
        :rtype: List[str]
        """
        ans = []
        trie = Trie()
        node = trie.root
        for w in words:
            trie.insert(w)
        
        for i in range(len(board)):
            for j in range(len(board[0])):
                self.dfs(board, i, j, node, "", ans)
        return ans

    def dfs(self, board, i, j, node, path, ans):

        if node.isword:
            ans.append(path)
            node.isword = False

        if i < 0 or i >= len(board) or j < 0 or j >= len(board[0]):
            return

        tmp = board[i][j]

        node = node.children.get(tmp)
        if not node:
            return 
        board[i][j] = '0'

        self.dfs(board, i+1, j, node, path+tmp, ans)
        self.dfs(board, i-1, j, node, path+tmp, ans)
        self.dfs(board, i, j+1, node, path+tmp, ans)
        self.dfs(board, i, j-1, node, path+tmp, ans)

        board[i][j] = tmp

0629 - Leetcode62 - Unique Paths

A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).

How many possible unique paths are there?

解题思路：

老动态规划题了，很直接的想法，因为一个点只能由它上面一个点或者左边的点到达，那么我们定义dp表示到每个点一共有几条路径。

定义动态规划矩阵：dp[i][j] 表示到达点 (i,j) 有几条unique的路径
状态转移方程： dp[i][j] = dp[i-1][j] + dp[i][j-1]

def uniquePaths(self, m, n):
        """
        :type m: int
        :type n: int
        :rtype: int
        """
        
        dp = [[0]*n for _ in range(m) ]
        
        dp[0][0] = 1
        for i in range(m):
            
            for j in range(n):
                if i == 0 or j == 0:
                    dp[i][j] = 1
                else:
                    dp[i][j] = dp[i-1][j] + dp[i][j-1]
                
        return dp[m-1][n-1]

补充 - Leetcode63 - Unique Paths II

A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).

Now consider if some obstacles are added to the grids. How many unique paths would there be?

解题思路：

考虑障碍，有障碍的地方就设为0

def uniquePathsWithObstacles(self, obstacleGrid):
        """
        :type obstacleGrid: List[List[int]]
        :rtype: int
        """
        m = len(obstacleGrid)
        n = len(obstacleGrid[0])
        
        dp = [[0]*n for _ in range(m)]
        dp[0][0] = 1 * (1 - obstacleGrid[0][0])
        for i in range(1, m):
            dp[i][0] = dp[i-1][0] * (1 - obstacleGrid[i][0])
        for j in range(1, n):
            dp[0][j] = dp[0][j-1] * (1 - obstacleGrid[0][j])
            
        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = (dp[i-1][j] + dp[i][j-1]) * (1 - obstacleGrid[i][j])
        
        return dp[m-1][n-1]

0628 - Leetcode322 - Reconstruct Itenerary

Given a list of airline tickets represented by pairs of departure and arrival airports [from, to], reconstruct the itinerary in order. All of the tickets belong to a man who departs from JFK. Thus, the itinerary must begin with JFK.

Note:

If there are multiple valid itineraries, you should return the itinerary that has the smallest lexical order when read as a single string. For example, the itinerary ["JFK", "LGA"] has a smaller lexical order than ["JFK", "LGB"].

All airports are represented by three capital letters (IATA code).

You may assume all tickets form at least one valid itinerary.

One must use all the tickets once and only once.

Example 1:
1
2
Input: [["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]]
Output: ["JFK", "MUC", "LHR", "SFO", "SJC"]

解题思路

DFS，试探走路。

def findItinerary(self, tickets):
        """
        :type tickets: List[List[str]]
        :rtype: List[str]
        """
        res = []
        
        paths = defaultdict(list)
        tickets.sort(key=lambda x: x[1], reverse=True)
        
        for d, a in tickets:
            paths[d].append(a)
            
        self.dfs('JFK', res, paths)
        
        return res[::-1]
        
        
    def dfs(self, d, res, paths):
        
        # res.append(d)
        arrivals = paths[d]
        while arrivals:
            self.dfs(arrivals.pop(), res, paths)
            
        res.append(d)

0627 - Leetcode279 - Perfect squares

Given a positive integer n, find the least number of perfect square numbers (for example, 1, 4, 9, 16, ...) which sum to n.

Example 1:
1
2
3
Input: n = 12
Output: 3 
Explanation: 12 = 4 + 4 + 4.
Example 2:
1
2
3
Input: n = 13
Output: 2
Explanation: 13 = 4 + 9.

解题思路：

动态规划。首先想到的就是动态规划，因为这道题和换零钱那道题太像了。但是做题的时候我不太能想起来换钱那道题是怎么做的了，就只记得换钱那道题考虑的是每一次，我这个1/2/5元的面值要不要参与其中。

所以这个题也差不多，刚开始的时候我想到的dp[i]是拥有i个square number的时候，可能组成的和的个数，这么一想的话，就有点像dfs了。所以我又换了个角度想了一下，dp[i]定义为：当和为i的时候，使用的最少的sqaure number有几个。

dp矩阵的含义：当和为i的时候，使用的最少的sqaure number有几个
状态转移方程： dp[i] = min(dp[i], dp[i-square_number] + 1)。状态转移方程这里说的是，我们dp[i]使用的square number的个数可以由 dp[i - square number]使用的个数 + 1得到。
我一开始是循环整数将所有可能的（平方小于等于n）的数都找了一遍，然后存储起来，但是这样的话时间复杂度超过了。所以这里直接用 range(1, int(n**0.5)+1)来代替。

def numSquares(self, n):
        """
        :type n: int
        :rtype: int
        """
        
        dp = [float('inf')]*(n+1)
        dp[0] = 0
        for i in range(1, n+1):
            dp[i] = min([dp[i - k**2] + 1 for k in range(1, int(n**0.5)+1)])
            
        return dp[-1]

DFS

DFS 的思路也很好想到，就是你冲着一个数字一直选，直到达到想要的和n，然后返回这条路径用了几个square number，如果达到的和超过了n那么这条路径放弃，最后选出最短路径。

0626 - Leetcode127 - Sum Root to Leaf Number

Given a binary tree containing digits from 0-9 only, each root-to-leaf path could represent a number.

An example is the root-to-leaf path 1->2->3 which represents the number 123.

Find the total sum of all root-to-leaf numbers.

Note: A leaf is a node with no children.

Example:
1
2
3
4
5
6
7
8
9
Input: [1,2,3]
    1
   / \
  2   3
Output: 25
Explanation:
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Therefore, sum = 12 + 13 = 25.
Example 2:
1
2
3
4
5
6
7
8
9
10
11
12
Input: [4,9,0,5,1]
    4
   / \
  9   0
 / \
5   1
Output: 1026
Explanation:
The root-to-leaf path 4->9->5 represents the number 495.
The root-to-leaf path 4->9->1 represents the number 491.
The root-to-leaf path 4->0 represents the number 40.
Therefore, sum = 495 + 491 + 40 = 1026.

解题思路：

Recursive：

我是用recursive写的，主要思路是尝试找到每一个leaf. 如果一个节点的左右子节点都是none，那么这个节点就是leaf，遇到了leaf之后，我们才能把它加到总结果上面。可以有两个方案，一个是将这些root-leaf的数字保存在list里面，然后最后返回list的和，另一个是直接用累加来记录。

需要注意的是 在做累加的时候，累加的参量一定是self.ans内部的变化量，不然再没有返回值的情况下，普通的变量是不会变化的。但是如果是都放在list里面，这个是可以的，可以将他们都保存起来，list在递归的过程中是一直变化的。这里的例子是按照path写的，因为可以提供更多的信息。

def sumNumbers(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        
        ans = []
        count = 0
        
        if not root:
            return 0
        
        self.dfs(root, count, ans)
        
        return sum(ans)
        
        
    def dfs(self, root, count):
        
        if not root.left and not root.right:
            count = 10*count + root.val
            ans.append(count)
            return 
        elif not root.right:
            count = 10*count + root.val
            self.dfs(root.left, count, ans)
        elif not root.left:
            count = 10*count + root.val
            self.dfs(root.right, count, ans)
        else:
                    
            count = 10*count + root.val

            self.dfs(root.left, count, ans)
            self.dfs(root.right, count, ans)

dfs+stack

这个思路是stack的顺序，然后改变每一个node的值为：到该点为止的累加值。

首先需要拿出root，然后放入stack中的数字是root的左右子节点，但是左右子节点对应的val的值分别存入的是 root.val*10 + root.right.val 和 root.val*10 + root.left.val,这样一直往stack里面放数字，如果左右子节点均为空，那么就用ans + 该点的val，如果左右子节点其中有一个为空，也不用管，直接return就可以。循环一直持续，直到stack中没有存储值。

（并没有改变树本身，而是在存在stack里面之后才改变了每个节点对应的value的值。）

def sumNumbers(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if not root:
            return 0
        
        stack = [(root, root.val)]
        res = 0

        while stack:

            root, val = stack.pop()
            
            if not root.left and not root.right:

                res += val

            if root.right:
                stack.append((root.right, val*10 + root.right.val))

            if root.left:
                stack.append((root.left, val*10 + root.left.val))

        return res

0625 - Leetcode287 - Find the Duplicate Number

Given an array nums containing n + 1 integers where each integer is between 1 and n (inclusive), prove that at least one duplicate number must exist. Assume that there is only one duplicate number, find the duplicate one.

Example 1:
1
2
Input: [1,3,4,2,2]
Output: 2
Example 2:
1
2
Input: [3,1,3,4,2]
Output: 3

解题思路：

我一开始想的都太肤浅了，这道题的要求是时间复杂度不大于 $O(n^2)$, 空间复杂度为$O(1)$。如果你普通得把见过一次的数字存在一个list里面，然后遍历整个序列的话，时间复杂度没超标但是空间复杂度超标了。

还有一种方法是可以用set，将nums进行set处理，然后nums和set过的nums求和做差，然后再除以两个nums的长度差。这种算法不知道算不算改变原有的nums，但同样也可以pass。

然后就来看看根正苗红的做法，可以用binary search来做。这里值得注意的是，题目中提到的，我们的nums的长度为n+1而nums中的数字都处于[1, …, n]。我们利用二分法查找来看多出来的这个duplicate数字究竟在哪里。

首先左右两端的端点定下来，然后寻找中间的数字。
之后查看nums中，小于等于中间这个数nums[mid]的数字个数，如果数字个数等于或者小于nums[mid], 这说明重复的数字出现在右侧，这时候更新left = mid + 1；否则的话更新right = mid。
这样我们的时间复杂度是 $O(nlogn)$, 空间复杂度是 $O(1)$

def findDuplicate(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        
        order = range(1, len(nums))
        
        left = 0
        right = len(order) - 1
        
        while left < right:
            mid = (left + right)/2
            
            count = 0
            
            for n in nums:
                if n <= order[mid]:
                    count += 1
            
            if count > order[mid]:
                right = mid
            else:
                left = mid + 1
        
        return order[left]

补充 - Leetcode142 - Linked List Cycle II

Given a linked list, return the node where the cycle begins. If there is no cycle, return null.

To represent a cycle in the given linked list, we use an integer pos which represents the position (0-indexed) in the linked list where tail connects to. If pos is -1, then there is no cycle in the linked list.

Note: Do not modify the linked list.

Example 1:
1
2
3
Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.

解题思路：

查看linked list里面有没有cycle就很直接，设两个pointer 一个一次走一步，一个一次走两步，看两个pointer会不会相遇，如果相遇，那么就说明有cycle，如果与一个pointer率先到达none，也就是最后的端点，那么这个linked list就是没有cycle
slow 和fast pointer相遇之后，要看一下这个cycle有多长，则固定fast不动，每次走一步slow，看走几步之后slow会和fast相遇，这时候得到了cycle中node的个数，也就是cycle的长度N
那就等于说，如果我们再设置两个pointer，一个比另一个多N步，那么他们会在某一个相遇，而相遇的位置就是cycle开始的位置。

def detectCycle(self, head):
        """
        :type head: ListNode
        :rtype: ListNode
        """
        if not head:
            return 
        
        fast = head
        slow = head
        while slow.next and fast.next and fast.next.next:
            fast = fast.next.next
            slow = slow.next
            # print(fast.val, slow.val)
            if fast == slow:
                step = slow.next
                count = 1
                p1 = head.next
                while step != slow:
                    step = step.next
                    p1 = p1.next
                    count += 1
                p2 = head
                s = 0
                while True:
                    if p1 == p2:
                        return p1
                    p1 = p1.next
                    p2 = p2.next
                    s += 1
            
                    
        return

0624 - Leetcode96 - Unique Binary Search Trees

Given n, how many structurally unique BST’s (binary search trees) that store values 1 … n?

解题思路：

初见这道题，我觉得肯定是用一个动态的思想去做，所以想到了dfs（怎么觉得dfs和dp的想法差不多呢，还是我自己没搞明白）

一开始我是想对于一个给定的数列nums，我可以分别以其中的一个数nums[i]为root，又因为是binary search tree，所以这个数字左边的部分nums[:i] 和右边的部分 nums[i+1:] 分别就在root的左边和右边。那么动态的去想一想，以nums[i]为root的BST的个数就等于nums[:i]的BTS个数加上nums[i+1:] 的BTS的个数。

但是！这里的加上是不对的，因为如果在nums = [1,2,3]，以2为root时，左边1有一种可能，右边三有一种可能，加起来就是两种可能，所以是不正确的。应该是乘上！！

好，那以nums[i]为root的BTS的个数就等于nums[:i]数列BTS的个数乘以 nums[i+1:]数列BTS的个数，然后我们遍历nums中所有的i，再把这些加起来。

这样就可以用DFS去做了。但是，我们还可以进一步的改进它。需要注意的是，我们的数列已经是顺序排列了，所以说，其实在计算BTS的个数的时候，我们不需要去担心数列里的数字是多少。比如，[1,2,3]和[4,5,6]生成的BTS的数目是一样的。所以我们在做DFS的时候，就会产生很多重复计算。这时候，我们就想到用DP了。

如果需要使用动态规划的算法，那么我们的一维dp[i]矩阵表示的就是，当数列的长度为i的时候，它存在的BTS的数目。

dp[i] - 当数列的长度为i的时候，它存在的BTS的数目
状态转移方程 - dp[i] = sum([dp[k] * dp[i-1-k] for k in range(i))

def numTrees(self, nums):
  
  dp = [0]*(n+1)
  
  dp[0] = 1 #一边为空时，所选方案为1种
  for i in range(1, len(dp)):
    
    for j in range(i):
      dp[i] += dp[j] * dp[i-1-j]
      
  return dp[-1]

# dfs  -> TLE
def numTrees(self, n):
        """
        :type n: int
        :rtype: int
        """
        nums = range(1, n+1)
        return self.dfs(nums, 0)

        
    def dfs(self, nums, count):
        
        if len(nums) == 0:
            return 1

        count = sum([self.dfs(nums[:i], count) * self.dfs(nums[i+1:], count) for i in range(len(nums))])
            
        return count

补充 - Leetcode95 - Unique Binary Search Tree II

Given an integer n, generate all structurally unique BST’s (binary search trees) that store values 1 … n.

Example:
1
2
3
4
5
6
7
8
9
Input: 3
Output:
[
  [1,null,3,2],
  [3,2,null,1],
  [3,1,null,null,2],
  [2,1,3],
  [1,null,2,null,3]
]

解题思路：

依循着上道题我的DFS的思路，看看能不能接着搞。

0623 - Leetcod222 - Count Complete Tree Node

Given a complete binary tree, count the number of nodes.

Note:

Definition of a complete binary tree from Wikipedia:
In a complete binary tree every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.

解题思路：

本来想用dfs做的，就计数遍历过的node。但没写出来。

只能用题目中给出的需要计算 tree的depth。

已知给定的是complete binary tree，那么一定是左子树都填满之后再填右子树，所以说左右子数的深度就很能说明问题。

如果左右子树的depth相同，那么左子树是满的，可能出现问题的只可能是右子树

如果左右子树的depth不同，那么右子树是满的，我们需要继续探索左子树看他究竟有几层。

def countNodes(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        
        if not root:
          return 0
        
        leftDepth = self.getDepth(root.left)
        rightDepth = self.getDepth(root.right)
        
        if leftDepth == rightDepth:
          return (2**leftDepth) + self.countNodes(root.right)
        else:
          return (2**rightDepth) + self.countNodes(root.left)
        
def getDepth(self, root):
  
    if not root:
      return 0

    return 1 + self.getDepth(root.left)

0622 - Leetcode137 - Single Number II

Given a non-empty array of integers, every element appears three times except for one, which appears exactly once. Find that single one.

Note:

Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?

Example 1:
1
2
Input: [2,2,3,2]
Output: 3
Example 2:
1
2
Input: [0,1,0,1,0,1,99]
Output: 99

解题思路：

直接解题：

我们已经知道，除了一位数字之外，其他的数字出现的次数都是三次，那么我们可以将这个list进行set处理，然后求和乘以三，再减去之前未作处理的list求和，之后再除以2就可以得到想要的数字。所以这是一行很简单的代码。
1
2
3
4
5
6
def singleNumber(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
return (3*sum(set(nums)) - sum(nums))//2

位运算：

我们可以利用二进制将数字都转化，所有出现三次的数字，他们的二级制也是一样的，所以说，每一位的和除以3一定是可以整除的，除非有一个其他的数字出来插一脚。所以我们的做法也很明确了，就是遍历所有位，然后对每一位的数求和并处以3，保存余数。以后再将这个二进制数还原为十进制整数。

这里的range从32中取值是因为整数最多为32位。最后一步说明当得到的数字是负数的时候，我们要用正数减去最大值得到负数。

def singleNumber(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        ans = 0
        for i in range(32):
            count = 0
            for j in nums:                
                count += (j>>i) & 1
            
            ans = ans | (count%3) << i
        
        return ans - 2**32 if ans>>31&1 == 1 else ans

补充 - Leetcode136 - Single Number I

Given a non-empty array of integers, every element appears twice except for one. Find that single one.

Note:

Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?

Example 1:
1
2
Input: [2,2,1]
Output: 1
Example 2:
1
2
Input: [4,1,2,1,2]
Output: 4

解题思路：

同样，这道题有很多解，第一个就是和之前一样，因为除了一个数字只出现一次之外，别的数字都出现两次，所以我们可以接着把这个list中的数字做set处理求和，然后乘以2再减去处理之前的list求和，就可以得到只出现一次的那个数值了。同样也可以看到一个数字的时候把它放进list中，如果再看见就把它从list用pop出来，最后list中剩下的那个数字就是我们要找的数值。

这里我们还是讲一下位运算。

如果两个数字相同，说明他们转化为二进制之后，每一位上的数字个数都是2，除了之前我们说的，可以将每一位求和除以出现的次数2，然后找余数之外。对于出现两次（偶数次）的数字，我们可以做xor处理，即两位相同返回0，不同返回1. 当我们对两个相同的数字 a 和数字 b做异或运算的时候，如果两个数字相同，那么a^b = 0, 否则的话肯定有一位是1。那么当我们对list中所有的数字做异或运算的时候，最后得到的结果就是多出来的那个数字。还有一个 0和任何数字做异或运算都等于他本身

def singleNumber(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        xor = 0
        for n in nums:
            xor ^= n
            
        return xor

补充 - Leetcode260 - Single Number III

Given an array of numbers nums, in which exactly two elements appear only once and all the other elements appear exactly twice. Find the two elements that appear only once.

Example:
1
2
Input:  [1,2,1,3,2,5]
Output: [3,5]

解题思路：

这一题和之前两个题不同之处在于，这里出现一次的数字不止一个了，而是两个，所以之前两个题用到的做set处理之后求和，然后再减去之前的list的和，这种方法就失效了。

我们还是来考虑位运算。

既然是位运算，那么我们还是来看一看xor运算能给我们带来什么。之前说过的是，如果两个数字相同，那么做了异或运算之后我们会得到0，对所有数字进行异或运算可以帮助我们得到唯一一个不同的数字。那既然我们现在有两个只出现一次的数字，就说明对所有数字做了异或运算之后，我们得到的是这两个数字异或运算后的结果。

这个结果也是很重要的，得到的结果至少有一位是1（即两个数字这这一位上是不同的）。那么我们要做的就是找到这一位pointer，然后将nums中的数字分为两个部分。一部分数字在pointer这一位都为0，另一部分数字再pointer这一位都为1，这样的话，这两个数字就会分别处在两个不同的部分。然后我们对每个部分分别作异或运算，就可以得到两个出现一次的数字了。

def singleNumber(self, nums):
        """
        :type nums: List[int]
        :rtype: List[int]
        """
        nxor = 0
        for n in nums:
            nxor = nxor ^ n
            
        for i in range(32):
            if (nxor >> i) & 1 == 1:
                pointer = i
                break
        # print(pointer)
        nums1 = []
        nums2 = []
        for n in nums:
            if (n >> pointer) & 1 == 1:
                nums1.append(n)
            else:
                nums2.append(n)
        # print(nums1, nums2)
        n1 = 0 
        n2 = 0
        for n in nums1:
            n1 = n1^n
            
        for n in nums2:
            n2 = n2^n
            
        return [n1, n2]

0621 - Leetcode174 - Dungeon Games

The demons had captured the princess (P) and imprisoned her in the bottom-right corner of a dungeon. The dungeon consists of M x N rooms laid out in a 2D grid. Our valiant knight (K) was initially positioned in the top-left room and must fight his way through the dungeon to rescue the princess.

The knight has an initial health point represented by a positive integer. If at any point his health point drops to 0 or below, he dies immediately.

Some of the rooms are guarded by demons, so the knight loses health (negative integers) upon entering these rooms; other rooms are either empty (0’s) or contain magic orbs that increase the knight’s health (positive integers).

In order to reach the princess as quickly as possible, the knight decides to move only rightward or downward in each step.

解题思路：（开心，是我自己徒手写的动态规划算法鸭）

这道题就是标准的动态规划的题目了。捋一捋思路。

涉及二维的，只能通过往右和往下两种路径到达终点的题目，肯定涉及走不同的路径，然后选取到该点的最小cost的类的问题，所以这类问题需要倒着推。
首先明确我们dp[i][j] 的意义，既然我们要求的是到达dungeon[i][j]的最小路径和，那么我们就将 dp[i][j] 表示为到达dungeon[i][j] 的最小cost和，而dungeon[i][j]就表示在[i][j]点的cost。
然后来找状态转移方程，我们到达[i][j]点至少消耗的体力值，等于我们在[i+1][j]点至少消耗的体力值 + 在 [i-1][j] 消耗/获得的体力值，或者是等于[i][j+1]点至少消耗的体力值 + 在 [i][j+1] 消耗/获得的体力值，至于选择从哪条路径来，就看哪条路径需要的体力值最小。

所以我们的状态转移方程为

dp[i][j] = min(dp[i+1][j] - dungeon[i][j], dp[i][j+1] - dungeon[i][j])
但有一点需要注意的是，如果 dungeon[i][j] 获得的体力值大于下一步即将消耗的体力值，那么我们其实获得将要消耗的体力值+1就可以了，因为如果过大，在之前的减法中，就会出现负数。举个例子：如果在dungeon[i+1][j]我们将会获得10点体力值，而到达dp[i][j]至少需要4点体力值的话，那么我们到达dp[i+1][j]时，至少需要有 -6点体力值，这是不可能的，因为如果体力值小于0，王子就死了。所以这个时候，我们到达dp[i+1][j]至少需要5点体力值，即dp[i+1][j]- dundeon[i][j]>= 1，所以我们的dp[i+1][j]-1 >= dundeon[i][j], 所以上一步的 dp[i][j] = min(dp[i+1][j] - dungeon[i][j], dp[i][j+1] - dungeon[i][j]) 换为：dp[i][j] = min(dp[i+1][j] - min(dungeon[i][j], dp[i+1][j]-1), dp[i][j+1] - min(dungeon[i][j], dp[i][j+1] - 1))
Initial Condition: dp右下角点的值，也就是营救公主所需要的生命力 = 1 - min(dungeon[M-1][N-1], 0)

def calculateMinimumHP(self, dungeon):
        """
        :type dungeon: List[List[int]]
        :rtype: int
        """
        M = len(dungeon)
        N = len(dungeon[0]) 
        
        dp = [[0]*N for _ in range(M)]
        
        for i in range(M-1, -1, -1):
            for j in range(N-1, -1, -1):

                if i == M-1 and j == N-1:
                    dp[i][j] = 1 - min(dungeon[M-1][N-1], 0) 
                elif i == M-1:
                    dp[i][j] = dp[i][j+1] - min(dungeon[i][j], dp[i][j+1] - 1)
                elif j == N-1:
                    dp[i][j] = dp[i+1][j] - min(dungeon[i][j], dp[i+1][j] - 1)
                else:                
                    dp[i][j] = min(dp[i+1][j] - min(dungeon[i][j], dp[i+1][j]-1), dp[i][j+1] - min(dungeon[i][j], dp[i][j+1] - 1))
        # print(dp)
        return dp[0][0]

0620 - Leetcode60 - Permuation Sequence

The set [1,2,3,...,*n*] contains a total of n! unique permutations.

By listing and labeling all of the permutations in order, we get the following sequence for n = 3:

"123"

"132"

"213"

"231"

"312"

"321"

Given n and k, return the kth permutation sequence.

解题思路：

暴力求解

这个方法的时间复杂度会比较高，可能会造成Limit Time exceeded的错误，但是这里想要指出的是permuation这类题的共性，所以在这里指出。

我们首先要知道的这个nums序列permutation变化的规律：

两个极端的例子是第一个permutation是从小到大依次排列的组合，第二个则是从大到小依次排列的组合。也就是说当我们的序列中存在非递减序列的时候，还是有下一次permute的可能性的，而当我们的序列已经是一个非递增序列的时候，这个permuation的过程就可以结束了。
我们要找的下一次permute的序列和本次序列的关系就是：找到本次序列中的非递增序列，然后将这个非递增序列的前一位（nums[pointer]）和非递增序列中稍大于这一位数字（nums[change]）的两项进行交换，最后顺序排列 nums[pointer+1::]

这种方法可以帮我们按照顺序求解出来所有的permutation，既然我们要找的是第k个permutation，那么就将此步骤重复k-1次（因为第一个permutation不计入）

def getPermutation(self, n, k):
        """
        :type n: int
        :type k: int
        :rtype: str
        """
        nums = range(1, n+1)
        for i in range(k - 1):
            # print(i, nums)
            self.nextPermutation(nums)
            
        return ''.join(str(k) for k in nums)
        
    def nextPermutation(self, nums):
        
        pointer = len(nums) - 1
        
        while pointer > 0:            
            if nums[pointer - 1] >= nums[pointer]:
                pointer -= 1
            else:
                break
        pointer -= 1        
        change = len(nums) - 1
        
        while change > pointer:            
            if nums[change] > nums[pointer]:                
                nums[change], nums[pointer] = nums[pointer], nums[change]
                nums[pointer+1::] = sorted(nums[pointer+1::])
                break
            change -= 1

直接按照可能出现的序列个数利用mod进行查找
1
2

补充 - Leetcode31 - Next Permutation

Implement next permutation, which rearranges numbers into the lexicographically next greater permutation of numbers.

If such arrangement is not possible, it must rearrange it as the lowest possible order (ie, sorted in ascending order).

The replacement must be in-place and use only constant extra memory.

Here are some examples. Inputs are in the left-hand column and its corresponding outputs are in the right-hand column.
1
2
3
>1,2,3` → `1,3,2`
>`3,2,1` → `1,2,3`
>`1,1,5` → `1,5,1

解题思路：

按照上面总结的permutation的规律就可以得到。需要注意的是，如果permutation已经是最后一个，即倒序排列时，需要返回的是正序的第一个序列。

def nextPermutation(self, nums):
        """
        :type nums: List[int]
        :rtype: void Do not return anything, modify nums in-place instead.
        """
        pointer = len(nums) - 1
        while pointer > 0:
            if nums[pointer-1] >= nums[pointer]:
                pointer -= 1
            else:
                break
        if pointer == 0:
            nums[0::] = nums[::-1]
            
            return 
        pointer -= 1
        
        change = len(nums) - 1
        while change > pointer:
            if nums[change] > nums[pointer]:
                nums[change], nums[pointer] = nums[pointer], nums[change]
                nums[pointer+1::] = sorted(nums[pointer+1::])
                return 
            change -= 1

0619 - Leetcode1044 - Longest Duplicate Substring

Given a string S, consider all duplicated substrings: (contiguous) substrings of S that occur 2 or more times. (The occurrences may overlap.)

Return any duplicated substring that has the longest possible length. (If S does not have a duplicated substring, the answer is "".)

Example 1:

1
2
Input: "banana"
Output: "ana"

Example 2:

1
2
Input: "abcd"
Output: ""

解题思路：

Rabin Carp + Binary Search

这题但凡是有一点的修改都会因为时间复杂度太高而无法通过。

首先来说说主要的想法Binary Search吧，个人感觉Rabin Carp只是为了降低搜索时候的时间复杂度而改变的。

这道题我们想要知道的是在string中重复出现的最长substring是什么。换个角度思考一下，如果我们给定了substring的长度，然后让你找这个长度下的substring有没有重复出现的，那么问题就会变得很清晰。这时候我们就可以用二分答案的方法来解决这个问题。假设最长substring的长度是m，那么substring长度为m-1， m-2，… 1的substring也会出现重复值。所以我们就可以用二分答案的方法来找到最长重复出现的substring。

当长度为length的substring找不到重复的时候，说明这个长度太长了，所以我们就更新右边的端点到mid
当长度为length的substring可以找到重复string的时候，说明我们能找到的substring可能比这个还长，所有我们就更新左边的端点到mid

其次就是 Rabin Carp，这个是把每个长度的substring用一个数字来表示，然后放在一个set里面，放在string里面并且判断这个数字是否在string中是不行的，会超过时间，set的计算效率是高于list的。

这个将string转化为一个数字的过程就是Rabin Carp算法。我们需要知道的是string中总共可能出现的数字是多少，然后将每个可能出现的字符用一个数字来表示。这里，所有可能出现的字符就是26个字母，所以a-0, b-1, c-2, …这些表示出来就可以了。个人觉得将这个string转化为数字就好像26进制一样，每个不同组合的string都会有对应的数字，然后再将这些数字储存在set中。为了防止重复出现的数字，我们将26进制转化后的数字mod by一个很大的数。

def longestDupSubstring(self, S):
        """
        :type S: str
        :rtype: str
        """
        A = [ord(c) - ord('a') for c in S]
        
        def testString(length, MOD):
    
            cur_hash = 0
            for i in range(mid):
                cur_hash = (cur_hash * 26 + A[i]) % MOD
                
            string_set = {cur_hash}
            max_pow = pow(26, length, MOD)
            for i in range(length, len(S)):
                # print(string_set)
                cur_hash = (cur_hash * 26 - A[i - length]*max_pow + A[i]) % MOD
                if cur_hash in string_set:
                    return i + 1 - length
                else:
                    string_set.add(cur_hash)
            return -1   
        
        left = 0
        right = len(S) - 1
        MOD = 2**63 - 1
        ans = ''
        while left <= right:
            mid = (left + right) // 2
            pos = testString(mid, MOD)
            # print(pos)
            if pos != -1:
                left = mid + 1
                ans = S[pos:pos+mid]
            else:
                right = mid - 1
                
        return ans

Suffix Array + Longest Common Prefix

这个方法就很巧妙了，主要是找到这个string从头开始的substring，然后再将这个substring排序，之后找这些substring里面最长的前缀。
- 首先需要提取字符串的所有suffix，也就是后缀。
  
  为什么要取后缀呢？因为按照brute borce的思想，假设我们先确定了一个字符i的位置，我们会做的是，在i后面的每一个字符起，开始遍历，试图去找一下是否有重复substring。所以我们要先把suffix提取出来
- 然后按照suffix的字母顺序进行排序。其实这个步骤就是隐性的帮我们把有重复项的suffix排在了一起，我们要做的就是找current suffix和它之后的suffix有多长重复的prefix（也就是当拿出两个已排好序的相邻的suffix从头进行比较，看两者最长的重复substring是什么）。
- 找出的最长prefix就被称作是Longest Common Prefix，这样也是可以解决这个问题的。
1

0618 - Leetcode275 - H-index II

Given an array of citations sorted in ascending order (each citation is a non-negative integer) of a researcher, write a function to compute the researcher’s h-index.

According to the definition of h-index on Wikipedia: “A scientist has index h if h of his/her N papers have at least h citations each, and the other N − h papers have no more than h citations each.”

Example:
1
2
3
4
5
6
Input: citations = [0,1,3,5,6]
Output: 3 
Explanation: [0,1,3,5,6] means the researcher has 5 papers in total and each of them had 
             received 0, 1, 3, 5, 6 citations respectively. 
             Since the researcher has 3 papers with at least 3 citations each and the remaining 
             two with no more than 3 citations each, her h-index is 3.

解题思路：

二分法查找：

首先明确目标：我们要找最小的能使 citations[i] >= len(citations) - i 的值

因为这里的citations中的数字都被排序了，所以我们可以使用二分法。

首先设置的是左右两边的pointer: left = 0, right = len(citations) - 1
设置循环条件：while left < right
更新：left = mid + 1; right = mid

更新的条件是判断citations[mid] >= len(citations) - mid

如果该条件成立，说明我们要找的点就在mid或是mid的左边(不一定mid这一点是最小的能满足这个条件的点)，所以这时我们更新right = mid

如果该条件不成立，即citations[mid] < len(citations) - mid，说明我们要找的点一定在mid的右边，所有我们更新 left = mid + 1
因为我们的循环条件是 while left < right 所以当left == right的时候，并没有审核citations[left]这个值符不符合要求，所以我们在最后需要再加上判别条件

if len(citations) == 0:
            return 0
                   
        left = 0
        right = len(citations) - 1
        
        while left < right:
            mid = (left + right)/2
            
            if citations[mid] >= len(citations) - mid:
                right = mid 
            else:
                left = mid + 1
        
        if citations[left] >= len(citations) - left:
            return len(citations) - left
        else:
            return len(citations) - (left+1)

Brute force：

设置pointer i从0开始，i代表的位置就是我们找到的最小的能使 citations[i] >= len(citations) - i 的值。

当 citations[i] < len(citations) - i的时候，意味着，在i点被引用的次数小于从i开始的文章数目，需要将i往后移动一位。
当 citations[i] >= len(citations) - i 的时候，意味着在i点，被引用的次数大于等于后面的文章数目了，所以此时我们已经找到了可以满足条件的i的位置，需要返回的是从i开始一共有几篇文章的数目，即len(citations) - i

def hIndex(self, citations):
        """
        :type citations: List[int]
        :rtype: int
        """
        i = 0
        while i < len(citations):
            if citations[i] >= len(citations) - i:
                return len(citations) - i
            else:
                i += 1
        return 0

0617 - Leetcode130 - Surrounded Regions

Given a 2D board containing 'X' and 'O' (the letter O), capture all regions surrounded by 'X'.

A region is captured by flipping all 'O's into 'X's in that surrounded region.

Explanation:

Surrounded regions shouldn’t be on the border, which means that any 'O' on the border of the board are not flipped to 'X'. Any 'O' that is not on the border and it is not connected to an 'O' on the border will be flipped to 'X'. Two cells are connected if they are adjacent cells connected horizontally or vertically.

解题思路：

这是一个联合分量的问题。

并不是说你网格中O的周围只要有一个是X，他就一定是X，，或者网格中的O周围有一个是O他就一定是O而是要看他边界的O是否相连接。

其实这里主要的一个思路是，如果网格中的O和边界上的O相连接，那么网格中的O就不用换成X，所以换个说法，我们在边界上寻找O，然后再看它和网格中间的哪些O相连，将这些O标记成新的量G，之后将所有没有被标记为G的O点，也就是不和外界相连的O点换成X。

用到的主要方法就是DFS，即我们寻找边界上的O，然后在他的上下左右方向寻找相连的O，将这些点标记为G。

def solve(self, board):
        """
        :type board: List[List[str]]
        :rtype: None Do not return anything, modify board in-place instead.
        """
        if len(board) <=2:
            return 
        
        def markG(i, j):
            
            if i < 0 or i >= len(board) or j < 0 or j >= len(board[0]) or board[i][j]!='O': return 
            else:
                board[i][j] = 'G'
                markG(i-1, j)
                markG(i+1, j)
                markG(i, j-1)
                markG(i, j+1)

        for i in range(len(board)):
            markG(i, 0)
            markG(i, len(board[0]) - 1)
            
        for j in range(len(board[0])):
            markG(0, j)
            markG(len(board) - 1, j)
            
            
        for i in range(len(board)):
            for j in range(len(board[0])):
                if board[i][j] == 'G':
                    board[i][j] = 'O'
                elif board[i][j] == 'O':
                    board[i][j] = 'X'

补充 - Leetcode200 - Number of Islands

Given a 2d grid map of '1's (land) and '0's (water), count the number of islands. An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.

Example 1:
1
2
3
4
5
6
7
Input:
11110
11010
11000
00000

Output: 1
Example 2:
1
2
3
4
5
6
7
Input:
11000
11000
00100
00011

Output: 3

解题思路：

这题和上一题是一样的，就是我们找到一个小岛之后，要把和它相连的部分都标记为“已遍历”，这里没有flag，就直接用一个别的符号来表示。然后当我们再次遇到这个点的时候就不会再遍历，造成重复。

唯一一点和上面一题不同的是，上面一题，只有和边界相接触的点才有可能被保存下来，但是这里只要是出现了1，我们就把他当做是一个岛。所以这里在写for循环的时候，需要遍历每一个为 1 的点，并且我们遇到1的时候count+1。count累加不能写在dfs函数的里面，我们在把和之前1相邻的点标记为“已遍历”的时候就会不停地累加。这个累加要出现在我们发现一个 1 的时候。

def numIslands(self, grid):
        """
        :type grid: List[List[str]]
        :rtype: int
        """
        if len(grid) == 0:
            return 0
        
        def markG(i, j):
            if i < 0 or i >= len(grid) or j < 0 or j>= len(grid[0]) or grid[i][j] != '1': return
            else:
                grid[i][j] = '2'
                markG(i+1, j)
                markG(i-1, j)
                markG(i, j+1)
                markG(i, j-1)
                
                
        count = 0
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                # print(grid)
                if grid[i][j] == '1':
                    count += 1
                    markG(i, j)
                    
        return count

补充 - Leetcode547 - Friend Circles

There are N students in a class. Some of them are friends, while some are not. Their friendship is transitive in nature. For example, if A is a direct friend of B, and B is a direct friend of C, then A is an indirect friend of C. And we defined a friend circle is a group of students who are direct or indirect friends.

Given a N*N matrix M representing the friend relationship between students in the class. If M[i][j] = 1, then the ith and jth students are direct friends with each other, otherwise not. And you have to output the total number of friend circles among all the students.

Example 1:

1
2
3
4
5
6
7
Input:
[[1,1,0],
[1,1,0],
[0,0,1]]
Output: 2
Explanation:The 0th and 1st students are direct friends, so they are in a friend circle.
The 2nd student himself is in a friend circle. So return 2.

Example 2:

1
2
3
4
5
6
7
Input:
[[1,1,0],
[1,1,1],
[0,1,1]]
Output: 1
Explanation:The 0th and 1st students are direct friends, the 1st and 2nd students are direct friends,
so the 0th and 2nd students are indirect friends. All of them are in the same friend circle, so return 1.

Note:

N is in range [1,200].

M[i][i] = 1 for all students.

If M[i][j] = 1, then M[j][i] = 1.

解题思路:

同样是用DFS搜索方法，但是和之前小岛不同的是，这里的是否交朋友是无序的，所以我们不能光考虑上下左右的边界，需要考虑的是所在行的所有数字。

def findCircleNum(self, M):
        """
        :type M: List[List[int]]
        :rtype: int
        """
        
        def markFriend(i):
            for k in range(len(M)):
                if M[i][k] == 1:
                    M[i][k] = 2
                    M[k][i] = 2
                    markFriend(k)         
                
        count = 0     
        for i in range(len(M)):
            if M[i][i] == 1:
                count += 1
                M[i][i] = 2
                markFriend(i)
                
        return count

0616 - Leetcode468 - Validate IP Address

Write a function to check whether an input string is a valid IPv4 address or IPv6 address or neither.

IPv4 addresses are canonically represented in dot-decimal notation, which consists of four decimal numbers, each ranging from 0 to 255, separated by dots (“.”), e.g.,172.16.254.1;

Besides, leading zeros in the IPv4 is invalid. For example, the address 172.16.254.01 is invalid.

IPv6 addresses are represented as eight groups of four hexadecimal digits, each group representing 16 bits. The groups are separated by colons (“:”). For example, the address 2001:0db8:85a3:0000:0000:8a2e:0370:7334 is a valid one. Also, we could omit some leading zeros among four hexadecimal digits and some low-case characters in the address to upper-case ones, so 2001:db8:85a3:0:0:8A2E:0370:7334 is also a valid IPv6 address(Omit leading zeros and using upper cases).

However, we don’t replace a consecutive group of zero value with a single empty group using two consecutive colons (::) to pursue simplicity. For example, 2001:0db8:85a3::8A2E:0370:7334 is an invalid IPv6 address.

Besides, extra leading zeros in the IPv6 is also invalid. For example, the address 02001:0db8:85a3:0000:0000:8a2e:0370:7334 is invalid.

Note: You may assume there is no extra space or special characters in the input string.

解题思路：

这个题看似简单，就是判断输入的字符串是IPv4还是IPv6，但实际太复杂了，这两种地址的条条框框太多了，一开始我是自己写的，后来test case实在无法通过，就参考了这里的写法。

我们就来分析一下：

IPv4
1. 当用 ‘.’ 将字符串split开的时候，长度必须为4（说的是有四个分开的部分，三个 ‘.’）
2. 每个split出来的字符串的都必须是数字，长度不能超过3，但是不能以0开头
3. 每个split出来的字符串中的数字不能为-1（谁能想到test case里面还有-1）
IPv6
1. 当用 ‘:’ 字符串split开的时候，长度必须是8
2. 每个split出来的字符串都必须是16进制，长度不能超过4，可以以0开头
3. 每个split出来的字符串中的数字不能为-1
最好用try except去做，不然其他的情况太多了，不能完全覆盖

def isIPv4(self, s):
    try: 
    #检查的是每个被 ‘.’ 隔离开的字符串
    # 1. str(int(s)) == s 检查字符串中的数字是否以0开头, 还可以避免-0的情况
    # 2. 0 <= int(s) <= 255 检查字符串中的数字是否在规定范围内
    	return str(int(s)) == s and 0 <= int(s) <= 255
    except: 
      return False

def isIPv6(self, s):
    if len(s) > 4: 
      return False
    try: 
      # int(s, 16) 是将s由16进制转化为十进制的整数
      return int(s, 16) >= 0 and s[0] != '-'
    except: 
      return False

def validIPAddress(self, IP):
    """
    :type IP: str
    :rtype: str
    """

    if IP.count(".") == 3 and all(self.isIPv4(i) for i in IP.split(".")): 
        return "IPv4"
    if IP.count(":") == 7 and all(self.isIPv6(i) for i in IP.split(":")): 
        return "IPv6"
    return "Neither"

0615 - Leetcode700 - Search in a binary tree

Given the root node of a binary search tree (BST) and a value. You need to find the node in the BST that the node’s value equals the given value. Return the subtree rooted with that node. If such node doesn’t exist, you should return NULL.

解题思路：

binary search tree

这里对于每个节点的左右进行搜索.因为binary search tree左右两边的node都是有大小顺序的，所以比较好排查，若果节点的val等于要找的value的值，那么就返回这个节点（所代表的tree），否则就一直往下找。

def searchBST(self, root, val):
        """
        :type root: TreeNode
        :type val: int
        :rtype: TreeNode
        """
                
        while root:
            if val == root.val:
                return root
            if val>root.val:
                root = root.right
            elif val<root.val:
                root = root.left

0614 - Leetcode787 - Cheapest Flights within K stops.

There are n cities connected by m flights. Each flight starts from city u and arrives at v with a price w.

Now given all the cities and flights, together with starting city src and the destination dst, your task is to find the cheapest price from src to dst with up to k stops. If there is no such route, output -1.

1
2
3
4
5
Example 1:
Input:
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 1
Output: 200

解题思路：

动态规划：

这题我一开始是想用动态规划来写的，但是这个dp矩阵我不知道怎么写。因为和之前的dp不同的是，图是无序的，所以无法用每个node的值来做横纵坐标，也就是说如果用城市的编号来写dp，然后每多走一步我们就滚动加上次的dp，是没法做的。

因此我琢磨了一下这道题对应的动态规划问题，也就是Bellman-ford’s方法，然后现在大概明白怎么进行了。

首先我们构建一个dp矩阵, dp[k][v] 代表在最多走k步的情况下，从起始点到点v的最短路程距离是多少。所以其实最终得到的dp矩阵可以告诉我们从src到每一个点的（最多走k步时）的路程距离，但最后返回的时候，我们只需要返回v = dst的值。

来看看动态规划问题：

子问题：当最多可以走k步时，从src到v的最短距离为：最多走k-1步，从src到v的最短距离以及最多走k-1步，src到u的最短距离+u到v的距离当中的最小值。
状态转移方程： dp[k][v] = min(dp[k-1][v], dp[k-1][u]+cost[u][v])

我们来看看图：

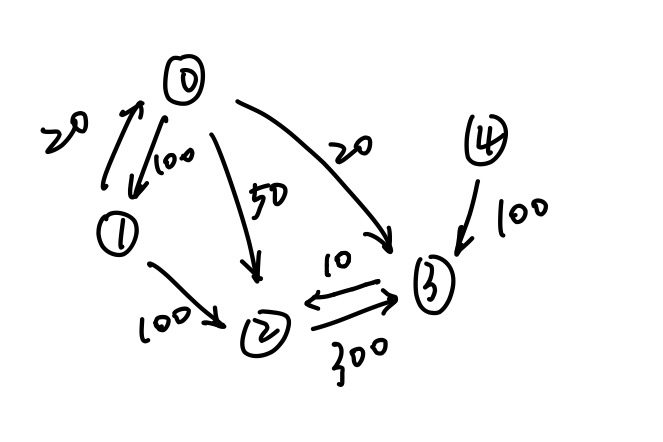
dp矩阵图：

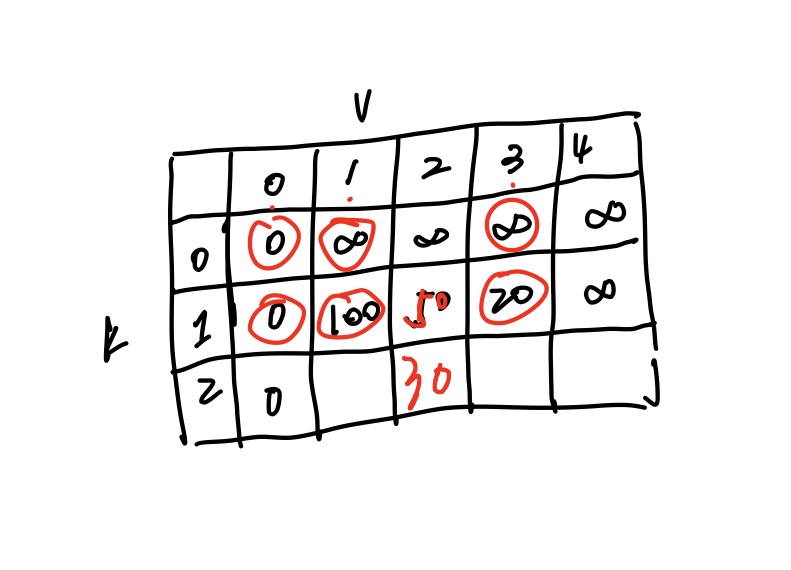
首先，规定我们的参数：src = 0, dst = 2, k = 1, n = 5, edge的长度如图所示。
明确几点common sense：
1. 因为我们的出发点是src，所以当v=src（终点等于起点）的时候，dp[k][src] = 0. 翻译一下，也就是说，当我们最多走k步的时候, src到自己的最短距离都是0
2. 因为我们考虑的情况是，当你走的步数变多，到达dst的距离可能会缩短，所以说，k-1步的距离肯定要大于等于k步的距离，即dp[k-1][dst] >= dp[k][dst]，所以dp[k][dst]的初始值就是dp[k-1][dst]。dp[k][dst] = dp[k-1][dst]表示多给出来我们走的那一步机会我们不用。
3. 如果要更新src到dst的距离，我们关心的是能到dst的点的上一步的最短距离。那这个例子来说，如果我们的dst为2，在更新的时候我们只关注src到0，1，3点的最短距离，因为只有这三个点可以到达2.所以我们在从edges这个list构建cost函数的时候也需要注意。如果不想考虑这些内容，那么没有连接的两个node之前的距离可以记做 $\infty$

def findCheapestPrice(self, n, flights, src, dst, K):
        """
        :type n: int
        :type flights: List[List[int]]
        :type src: int
        :type dst: int
        :type K: int
        :rtype: int
        """
        cost = {}
        for i in range(n):
            cost[i] = {}
            
        for f in flights:
            cost[f[1]][f[0]] = f[2]
            
        dp = [[float('Inf')]*n for _ in range(K+2)]
        dp[0][src] = 0
        
        for i in range(1, K+2):
            for j in range(n):
                if j == src:
                    dp[i][j] = 0
                else:
                    dp[i][j] = dp[i-1][j]
                    for u in cost[j]:
                        # print(dp[i-1][u]+cost[j][u], dp[i-1][j])
                        dp[i][j] = min(dp[i-1][u]+cost[j][u], dp[i][j])
                        # print(dp[i][j])
                        
        if dp[K+1][dst] == float('Inf'):
            return -1
        
        return dp[K+1][dst]

深度优先搜索

0613 - Leetcode368 - Largest Divisible Subset

Given a set of distinct positive integers, find the largest subset such that every pair (Si, Sj) of elements in this subset satisfies:

Si % Sj = 0 or Sj % Si = 0.

If there are multiple solutions, return any subset is fine.

解题思路：

排序之后 + 动态规划

排序的原因：假设 $a<b<c$ ，如果 $b\%a = 0$ 且 $c\%b = 0$, 那么我们就不用计算 $c \% a = 0$, 而且在排序之后不会出现被除数比除数大的情况。
动态规划子问题：假设我们用sol[k]来表示，输入数列中nums中的第l个数字对应的最长divisible序列。那么对于第j个数字，sol[j]的序列将会是 sol[i] + nums[j], where nums[j]%nums[i] == 0.
状态转移方程：sol[j] = sol[i] + nums[j]

注意这里需要有两个限定条件： 1. nums[j]%nums[i] == 0，这点是必须的，用来寻找nums[j]的可整除项；2. len(sol[j]) + 1 > len(sol[i]) ，这个在判定当前sol[j]的序列的长度加上nums[i] 是否大于sol[j]来已经有的序列长度。

万万不可 在找到了nums[j]%nums[i] == 0 就break啊，这样的话可能会错失更长的序列。比如，[4, 8, 10, 240] 这个就会输出 [10, 240]而不是[4, 8, 240]了

def largestDivisibleSubset(self, nums):
        """
        :type nums: List[int]
        :rtype: List[int]
        """
        if len(nums) == 0:
            return []
        
        nums = sorted(nums)
        sol = [[num] for num in nums]
        
        for i in range(len(nums)):
            j = i - 1
            while j >= 0:
                if nums[i] % nums[j] == 0 and len(sol[j]) + 1 > len(sol[i]):
                    sol[i] = sol[j] + [nums[i]]
                    
                j -= 1
                    
        return max(sol, key=len)

补充 - Leetcode300 - Longest Increasing Subsequence

Given an unsorted array of integers, find the length of longest increasing subsequence.

Example:

1
2
3
Input: [10,9,2,5,3,7,101,18]
Output: 4
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.

解题思路：

和上面lc368是一样的哦，只不过这里不涉及排序的问题，直接用动态规划就好了。
subsequence不意味着数字要连起来，所以和之前一样，也要遍历当前项之前的所有可能序列。

def lengthOfLIS(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        if len(nums) == 0:
            return 0
        
        sol = [[num] for num in nums]
        
        for i in range(1, len(nums)):
            j = i - 1
            while j >= 0:
                if nums[j] < nums[i] and len(sol[j])+1 > len(sol[i]):
                    sol[i] = sol[j] + [nums[i]]
                    
                j -= 1
                
        return max([len(s) for s in sol])

0612 - Leetcode380 - Insert Delete GetRandom O(1)

Design a data structure that supports all following operations in average O(1) time.

insert(val): Inserts an item val to the set if not already present.

remove(val): Removes an item val from the set if present.

getRandom: Returns a random element from current set of elements. Each element must have the same probability of being returned.

解题思路：

重点就是要用基本的数据结构去解决问题。这里用到了dictionary，可以用dictionary的key来存储值，value来存储位置，因为同一个数值只能出现一次，所以可以很好的运用dictionary.

import random
class RandomizedSet(object):

    def __init__(self):
        """
        Initialize your data structure here.
        """
        self.nums = []
        self.pos = {}
        

    def insert(self, val):
        """
        Inserts a value to the set. Returns true if the set did not already contain the specified element.
        :type val: int
        :rtype: bool
        """
        
        if val not in self.nums:
            self.pos[val] = len(self.nums) 
            self.nums.append(val)
            return True
        return False
        

    def remove(self, val):
        """
        Removes a value from the set. Returns true if the set contained the specified element.
        :type val: int
        :rtype: bool
        """
        
        if val in self.nums:
            idx = self.pos[val]
            self.nums[idx], self.nums[-1] = self.nums[-1], self.nums[idx]
            self.pos[self.nums[idx]] = idx
            del self.pos[self.nums[-1]]
            
            self.nums.pop()
            return True
            
        return False
        

    def getRandom(self):
        """
        Get a random element from the set.
        :rtype: int
        """
        idx = random.randint(0, len(self.nums)-1)
        return self.nums[idx]

0611 - Leetcode75 - Sorting Colors - Medium

Given an array with n objects colored red, white or blue, sort them in-place so that objects of the same color are adjacent, with the colors in the order red, white and blue.

Here, we will use the integers 0, 1, and 2 to represent the color red, white, and blue respectively.

Note: You are not suppose to use the library’s sort function for this problem.

Example:
1
2
Input: [2,0,2,1,1,0]
Output: [0,0,1,1,2,2]

解题思路：

因为存在三种颜色，所以用两次排序并且记录每个数字的个数是可以重新覆盖掉这个数组
存在三种颜色，我们可以用两个pointer分别从左右两端出发，左边的pointer卡在左侧1的位置，右边的pointer卡在右侧1的位置。还有一个pointer用来遍历。

注意：控制循环的条件是k <=j，因为j移动的位置是已经排序过的，所以大于j的部分不需要考虑。考虑等于j是因为j所在的位置也还没有考虑，所以需要控制 k<=j.

如果考虑 i < j 会出现移动的pointer k一直往后移动，导致大于j的已经排序好的部分被打乱。

def sortColors(self, nums):
    """
    :type nums: List[int]
    :rtype: None Do not return anything, modify nums in-place instead.
    """
    i = 0
    j = len(nums) - 1
    
    k = 0
    while k <= j:
        if nums[k] < 1:
            nums[k], nums[i] = nums[i], nums[k]
            k += 1
            i += 1
        elif nums[k] == 1:
            k += 1
        elif nums[k] > 1:
            nums[k], nums[j] = nums[j], nums[k]
            j -= 1

0610 - Leetcode35 - Search Insert Position - Easy

详解看这里

0609 - Leetcode392 - Is Subsequence

Given a string s and a string t, check if s is subsequence of t.

A subsequence of a string is a new string which is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, "ace" is a subsequence of "abcde" while "aec" is not).

Example 1:

1
2
Input: s = "abc", t = "ahbgdc"
Output: true

Example 2:

1
2
Input: s = "axc", t = "ahbgdc"
Output: false

重点：

从利用两个pointer的角度，是一道比较简单的题，直接按顺序跑一遍就行。
从动态规划的角度，要考虑如何把这个问题想象成一个子问题。

解题思路：

Pointer.

在string和target里面分别设置两个pointer，然后遍历target里面的所有值，直到在string中都找到相应的值即可。

def isSubsequence(self, s, t):
        """
        :type s: str
        :type t: str
        :rtype: bool
        """
        if len(s) > len(t):
            return False
        i = 0
        j = 0
        while i<len(s) and j<len(t):
            if s[j] == s[i]:
                i += 1
            j += 1
        if i == len(s):
            return True
        
        return False

动态规划

动态规划矩阵: dp[i][j] 代表string[:i] 中是否包含target[:j]
子问题：dp[i][j] 是否为True取决于dp[i-1][j-1] 以及string[i]和target[j]
状态转移方程：
- 当string[i]==target[j]时，若dp[i-1][j-1]为True，那么dp[i][j]也为True
- 当string[i]!=target[j]时，相当于此时string[i]是没用的，我们需要看dp[i-1][j]是否为True（表示当我们忽略掉string[i]的时候，string[:i-1] 中是否包含target[:j]）

def isSubsequence(self, s, t):
    """
    :type s: str
    :type t: str
    :rtype: bool
    """
    dp = [[False]*(len(t)+1) for _ in range(len(s)+1)]
    dp[0][0] = True
    for j in range(len(t)+1):
        dp[0][j] = True
        
    for row in range(1, len(s)+1):
        for col in range(1, len(t)+1):
            if s[row - 1] == t[col - 1]:
                dp[row][col] = dp[row - 1][col - 1]                    
            else:
                dp[row][col] = dp[row][col - 1]
                
    return dp[-1][-1]

补充 - Leetcode115 - Distinct Subsequence - Hard

Given a string S and a string T, count the number of distinct subsequences of S which equals T.

A subsequence of a string is a new string which is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, "ACE" is a subsequence of "ABCDE" while "AEC" is not).

It’s guaranteed the answer fits on a 32-bit signed integer.

Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
Input: S = "rabbbit", T = "rabbit"
Output: 3
Explanation:
As shown below, there are 3 ways you can generate "rabbit" from S.
(The caret symbol ^ means the chosen letters)

rabbbit
^^^^ ^^
rabbbit
^^ ^^^^
rabbbit
^^^ ^^^

Example 2:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Input: S = "babgbag", T = "bag"
Output: 5
Explanation:
As shown below, there are 5 ways you can generate "bag" from S.
(The caret symbol ^ means the chosen letters)

babgbag
^^ ^
babgbag
^^ ^
babgbag
^ ^^
babgbag
^ ^^
babgbag
^^^

解题思路：

动态规划：

动态规划矩阵： dp[i][j]表示string[:i] 中否包含target[:j]的不同组合个数
子问题：dp[i][j] 代表的个数取决于dp[i-1][j-1] 以及string[i]和target[j]
状态转移方程：
- 当string[i] == target[j] 时，dp[i][j] = dp[i-1][j-1] + dp[i][j-1] 表示当前两个字符相同的时候，现有组合数为dp[i-1][j-1] 加上dp[i][j-1] （考虑或者不考虑string[i]）
- 当string[i] ！= target[j]时，dp[i][j] = dp[i][j-1] 表示只能跳过target[i] 看看 string[:i]能不能在target[:j-1]中出现了几次。

def numDistinct(self, s, t):
        """
        :type s: str
        :type t: str
        :rtype: int
        """
        M = len(s)
        N = len(t)
        
        dp = [[0]*(M+1) for _ in range(N+1)]

        dp[0]= [1]*(M+1)
        
        for i in range(1, N+1):
            for j in range(1, M+1):
                if t[i-1] == s[j-1]:
                    dp[i][j] = dp[i-1][j-1] + dp[i][j-1]
                else:
                    dp[i][j] = dp[i][j-1]
                    
        return dp[N][M]

0608 - Leetcode231-Power Of Two - Easy

Given an integer, write a function to determine if it is a power of two.

1
2
3
>Input: 1
>Output: true
>Explanation: 2^0 = 1

重点：

注意输入小于等于零的状况
注意在递归时的return标记

解题思路：

Iteration

def isPowerOfTwo(self, n):
        """
        :type n: int
        :rtype: bool
        """
        if n <= 0:
            return False
        
        while n > 0:
            
            if n == 1:
                return True
            if n % 2 == 1:
                return False
            
            n = n / 2
            
        return True

Recursive

def isPowerOfTwo(self, n):
        """
        :type n: int
        :rtype: bool
        """
        if n <= 0:
            return False
        if n == 1:
            return True
        if n % 2 == 1:
            return False
        
        return self.isPowerOfTwo(n/2)

0607 - Leetcode518 - Coin Change 2

You are given coins of different denominations and a total amount of money. Write a function to compute the number of combinations that make up that amount. You may assume that you have infinite number of each kind of coin.

1
2
3
4
5
6
7
Input: amount = 5, coins = [1, 2, 5]
Output: 4
Explanation: there are four ways to make up the amount:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

重点：

因为每个币值的coin的数量是无限的，所以我们在选择换零钱方案的时候，都可以选择使用或者不使用该币值的coin。
首先想到的方法是循环，但在循环的过程中也会产生重复的计算过程会超过time limit，所以提示我们可以用动态规划。

解题思路：

递归

def change(self, amount, coins):
        """
        :type amount: int
        :type coins: List[int]
        :rtype: int
        """ 
        return self.countSol(amount, coins, 0)
    
    def countSol(self, amount, coins, i):
        
        if amount == 0: return 1
        if amount < 0: return 0
        if i > len(coins) - 1 and amount > 0:return 0
        return self.countSol(amount - coins[i], coins, i) + self.countSol(amount, coins, i + 1)

动态规划

动态规划的思路和刚才的递归的思路相似，但要如何构建DP空间呢？

之前我们所找到的状态转移方程是：某一(amount, coins)的方案数 = 考虑(coins[0])的状态数 + 不考虑该(coins[0]))的状态数。

假设一维动态矩阵dp[i], dp[i]表示：为了得到amount为i的结果，目前的coin有几种表达形式。

初始化： dp = [0]*(amount+1) 表示在没有coin的时候，生成i>0每一种结果的方式都是0. 除了 dp[0] = 1.

第一次循环：考虑coin[0]，在更新dp[i]之前，dp[i] 本身表示的就是生成该amount为i的方案中，不考虑coin[0] 时，我们有几种方法，而更新后的dp[i]还要加上dp[i-coin[0]]，表示拥有coin[0]之后，dp[i-coin[0]]个方法也可以被我们所用到了。

之后的循环都是一样的方法。

要注意的是，当在第j次循环下，如果 coin[j] > i, 即coin[j]本身币值的大小，大于所需的amount值，那么新考虑的coin[j]对这些amount是没影响的。

def change(self, amount, coins):
        """
        :type amount: int
        :type coins: List[int]
        :rtype: int
        """ 
        dp = [0]*(amount+1)
        dp[0] = 1
        for i in range(len(coins)):
            for j in range(1, amount+1):
                if coins[i] <= j:
                    dp[j] = dp[j] + dp[j - coins[i]]
        return dp[-1]

补充 - LeetCode322 - Coin Change

You are given coins of different denominations and a total amount of money amount. Write a function to compute the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.

Example 1:

1
2
3
Input: coins = [1, 2, 5], amount = 11
Output: 3
Explanation: 11 = 5 + 5 + 1

Example 2:

1
2
Input: coins = [2], amount = 3
Output: -1

解题思路：

和之前的一样，考虑动态规划问题，划分成subproblem，当前amount可得到的最小数量的coin和为（当前最小数量，dp[amount-coin[i]]+1）中的最小值。

重点：

初始化的时候每一项初始化为 amount +1, 因为amount最多需要amount数量的coin
在判断能否生成该amount时只需判断dp[amount]是否仍为amount+1即可。

def coinChange(self, coins, amount):
        """
        :type coins: List[int]
        :type amount: int
        :rtype: int
        """
        
        dp = [amount+1]*(amount+1)
        dp[0] = 0
        
        for i in range(len(coins)):
            for j in range(1, amount+1):
                if j >= coins[i]:
                    dp[j] = min(dp[j - coins[i]] + 1, dp[j])
         
        if dp[amount] == (amount+1):
            return -1
        
        return dp[-1]

0606 - Leetcode1029 - Two City Scheduling - Easy

There are 2N people a company is planning to interview. The cost of flying the i-th person to city A is costs[i][0], and the cost of flying the i-th person to city B is costs[i][1].

Return the minimum cost to fly every person to a city such that exactly N people arrive in each city.

1
2
3
4
5
6
7
8
9
Input: [[10,20],[30,200],[400,50],[30,20]]
Output: 110
Explanation:
The first person goes to city A for a cost of 10.
The second person goes to city A for a cost of 30.
The third person goes to city B for a cost of 50.
The fourth person goes to city B for a cost of 20.

The total minimum cost is 10 + 30 + 50 + 20 = 110 to have half the people interviewing in each city.

解题思路：

1 - 遍历+排序

假设全部人被送往A，则我们的花费为 $\sum\limits_{i = 1}^{2N}cost[i][0]$。

那我们的任务就变换为，从这A个人中挑选出来N个人，使他们的refund$ \sum\limits_{j=(1)}^{(N)}(- cost[i][0] + cost[i][1])$达到最大值。所以要做的就很简单，是把所有人的refund找出来，然后挑选前N个最大的。

（如果第$i$ 个人不去A了，改成去B，那么我们可以省去$cost[i][0] - cost[i][1]$这么多钱，省得越多越好）

def twoCitySchedCost(self, costs):
        """
        :type costs: List[List[int]]
        :rtype: int
        """
        costA = sum([c[0] for c in costs])
        save = [c[0] - c[1] for c in costs]
        
        save.sort()

        return costA - sum(save[len(costs)/2:])

2 - 动态规划

假设一个 $N \times N$ 的矩阵为DP矩阵，dp[i][j] 表示当i个人去A， j个人去B时的cost，所以dp矩阵的最后一项 dp[N][N] 代表N个人去A， N个人去B的cost。

初始状态：第0行中的dp[0][j] 表示0个人去A，j个人去B；同样 dp[i][0]表示i个人去A， 0个人去B。
状态转移方程：